-
-
宋宋 数据领袖Lv6
发表于2020-5-12 14:15
楼主
本帖最后由 宋宋 于 2020-5-12 14:17 编辑
在面对一组数据时,我们可以通过一些简单的指标来知道数据的趋势,这里的趋势主要有两种:集中趋势和离中趋势。
1 集中趋势
在统计学上,集中趋势是指一组数据向某一中心值靠拢的程度,它反映了一组数据中心点的位置所在,根据定义,集中趋势测度通常就是寻找数据水平的代表值或者中心值。在数据量巨大的时候,需要一些确切的指标来表明其整体状态。比较常见的就是平均数、分位数和众数。
1.1 平均数
平均数是描述定量数据的集中趋势,主要适用于定量数据。考虑最简单的算术平均数,定义如下:
一个数列的平均数等于它们的和除以它们所含数据的个数,记为 ,计算公式为:
,计算公式为:

R语言中的计算方法如下:
> a <- c(1,2,3,4,5,1,58,10)> mean(a)[1] 10.5>
a 数列含有8个数,总和为84,平均为10.5,采用mean()函数。
1.2 分位数
分位数是根据处在数列中点的位置来进行取值,比如一组数据按大小顺序排列后,处在数列中点位置的数值称为中位数,中位数将数据从中间一个点平均分成两部分,与中位数相对应的还有四分位数、十分位数和百分位数。它们分别是用3个点、9个点和99个点将数据四等分、十等分和一百等分。这里我们着重讨论四分位数。
从分位数的定义可以看出,以中位数为例,在计算之前首先需要将数据进行排序,然后根据数组的总个数和分位序数再从原数组当中读取具体的分位数数值。
实数 按大小顺序(升序、降序都可以)排列为
按大小顺序(升序、降序都可以)排列为  ,则实数数列x={
,则实数数列x={  }的中位数
}的中位数  为
为
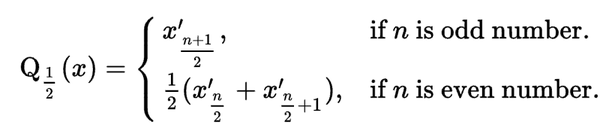
odd number为奇数,even number为偶数。
R语言中分位数的计算方法如下:
quantile(x, probs = seq(0, 1, 0.25), na.rm = FALSE, names = TRUE, type = 7, ...)#特别的,对于中位数有median()函数,直接求取中位数> median(x)[1] 2.5>
其中quantile()可以计算分位数,x为需要计算分位数的数组,probs参数可以给出(0,1)之间的分为间隔,比如0,0.25,0.5,0.75,1,0.5对应中位数,0.25则对应第一四分位数,0.75对应第三四分位数。下面举quantile()函数的例子:
> x<-c(1,2,3,4)> quantile(x) 0% 25% 50% 75% 100% 1.00 1.75 2.50 3.25 4.00 > quantile(x,probs=(0.5))50% 2.5 > quantile(x,probs=(0.2))20% 1.6 >
1.3 众数
众数是指一组数据中出现次数最多的变量,主要适用于分类数据。
主要特点是不受极值影响,但对于一组数据,众数可能并不唯一,有可能有多个众数,也有可能没有众数。
比较遗憾的是R中没有直接的内置函数来计算众数,不过可以根据定义简单地写一个,以下的代码参考自
# Create the function.getmode <- function(v) { uniqv <- unique(v) uniqv[which.max(tabulate(match(v, uniqv)))]}# Create the vector with numbers.v <- c(2,1,2,3,1,2,3,4,1,5,5,3,2,3)# Calculate the mode using the user function.result <- getmode(v)print(result)[1] 2# Create the vector with characters.charv <- c("baidu.com","tmall.com","yiibai.com","qq.com","yiibai.com")# Calculate the mode using the user function.result <- getmode(charv)print(result)
2 离中趋势
对一组数据总体特征的描述除了集中趋势,还需要了解数据组的分布偏离中心的程度,用以说明集中趋势测度值对所概括的数据的代表性大小。因此,在运用集中趋势测度值反映数据集中趋势的同时,还需要观察数据的离中程度,即离中趋势。这里主要介绍标准差和标准分。
2.1 标准差
标准差(SD),数学符号 σ(sigma),在概率统计中最常使用作为测量一组数值的离散程度之用。标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
标准差定义:为方差开算术平方根,反映组内个体间的离散程度;标准差与期望值之比为标准离差率。测量到分布程度的结果。
标准差的计算公式如下:

在R中可以sd()函数来计算标准差,举例如下:
> A <- c(12,23,34,44,59,70,98)> A[1] 12 23 34 44 59 70 98> sd(A)[1] 29.54013>
2.2 标准分
我们定义数组 他们的平均值为μ,标准差为σ,那么我们可以求出
他们的平均值为μ,标准差为σ,那么我们可以求出  的标准分
的标准分
z1 = (x1-μ)/σ (标准差不为0)
Z值的量代表着原始分数和母体平均值之间的距离,是以标准差为单位计算。在原始分数低于平均值时Z则为负数,反之则为正数。
在R中可以用scale()函数来计算标准分,
来源互联网
在面对一组数据时,我们可以通过一些简单的指标来知道数据的趋势,这里的趋势主要有两种:集中趋势和离中趋势。
1 集中趋势
在统计学上,集中趋势是指一组数据向某一中心值靠拢的程度,它反映了一组数据中心点的位置所在,根据定义,集中趋势测度通常就是寻找数据水平的代表值或者中心值。在数据量巨大的时候,需要一些确切的指标来表明其整体状态。比较常见的就是平均数、分位数和众数。
1.1 平均数
平均数是描述定量数据的集中趋势,主要适用于定量数据。考虑最简单的算术平均数,定义如下:
一个数列的平均数等于它们的和除以它们所含数据的个数,记为
R语言中的计算方法如下:
> a <- c(1,2,3,4,5,1,58,10)> mean(a)[1] 10.5>
a 数列含有8个数,总和为84,平均为10.5,采用mean()函数。
1.2 分位数
分位数是根据处在数列中点的位置来进行取值,比如一组数据按大小顺序排列后,处在数列中点位置的数值称为中位数,中位数将数据从中间一个点平均分成两部分,与中位数相对应的还有四分位数、十分位数和百分位数。它们分别是用3个点、9个点和99个点将数据四等分、十等分和一百等分。这里我们着重讨论四分位数。
从分位数的定义可以看出,以中位数为例,在计算之前首先需要将数据进行排序,然后根据数组的总个数和分位序数再从原数组当中读取具体的分位数数值。
实数
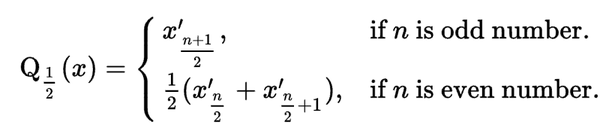
R语言中分位数的计算方法如下:
quantile(x, probs = seq(0, 1, 0.25), na.rm = FALSE, names = TRUE, type = 7, ...)#特别的,对于中位数有median()函数,直接求取中位数> median(x)[1] 2.5>
其中quantile()可以计算分位数,x为需要计算分位数的数组,probs参数可以给出(0,1)之间的分为间隔,比如0,0.25,0.5,0.75,1,0.5对应中位数,0.25则对应第一四分位数,0.75对应第三四分位数。下面举quantile()函数的例子:
> x<-c(1,2,3,4)> quantile(x) 0% 25% 50% 75% 100% 1.00 1.75 2.50 3.25 4.00 > quantile(x,probs=(0.5))50% 2.5 > quantile(x,probs=(0.2))20% 1.6 >
1.3 众数
众数是指一组数据中出现次数最多的变量,主要适用于分类数据。
主要特点是不受极值影响,但对于一组数据,众数可能并不唯一,有可能有多个众数,也有可能没有众数。
比较遗憾的是R中没有直接的内置函数来计算众数,不过可以根据定义简单地写一个,以下的代码参考自
# Create the function.getmode <- function(v) { uniqv <- unique(v) uniqv[which.max(tabulate(match(v, uniqv)))]}# Create the vector with numbers.v <- c(2,1,2,3,1,2,3,4,1,5,5,3,2,3)# Calculate the mode using the user function.result <- getmode(v)print(result)[1] 2# Create the vector with characters.charv <- c("baidu.com","tmall.com","yiibai.com","qq.com","yiibai.com")# Calculate the mode using the user function.result <- getmode(charv)print(result)
2 离中趋势
对一组数据总体特征的描述除了集中趋势,还需要了解数据组的分布偏离中心的程度,用以说明集中趋势测度值对所概括的数据的代表性大小。因此,在运用集中趋势测度值反映数据集中趋势的同时,还需要观察数据的离中程度,即离中趋势。这里主要介绍标准差和标准分。
2.1 标准差
标准差(SD),数学符号 σ(sigma),在概率统计中最常使用作为测量一组数值的离散程度之用。标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
标准差定义:为方差开算术平方根,反映组内个体间的离散程度;标准差与期望值之比为标准离差率。测量到分布程度的结果。
标准差的计算公式如下:
在R中可以sd()函数来计算标准差,举例如下:
> A <- c(12,23,34,44,59,70,98)> A[1] 12 23 34 44 59 70 98> sd(A)[1] 29.54013>
2.2 标准分
我们定义数组
z1 = (x1-μ)/σ (标准差不为0)
Z值的量代表着原始分数和母体平均值之间的距离,是以标准差为单位计算。在原始分数低于平均值时Z则为负数,反之则为正数。
在R中可以用scale()函数来计算标准分,
来源互联网




